Power in AC Circuit

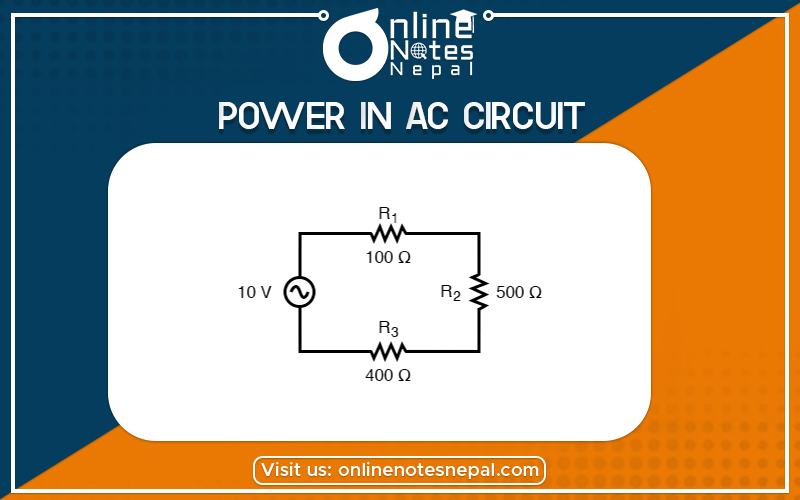
The power in the AC circuit is explained below:

AC circuits are usually three-phase for electrical distribution and electrical transmission purposes. Single-phase circuits are commonly used in our domestic supply system.

The total power of a three-phase AC circuit is equal to three times the single-phase power.

So if the power in a single phase of a three-phase system is ‘P’, then the total power of the three-phase system would be 3P (provided the three-phase system is perfectly balanced).

But if the three-phase system is not exactly balanced, then the total power of the system would be the sum of the power of individual phases.

Suppose, in a three-phase system, the power at R phase is PR, at Y phase is PY and at B phase is PB, then total power of the system would be

This is a simple scalar sum since power is a scalar quantity. This is the season if we consider only single-phase during calculating and analyzing of three-phase power, it is enough.

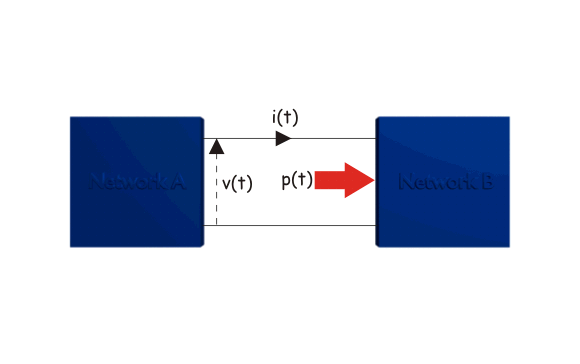
Let us consider, network A is electrically connected with network B as shown in the figure below:

Let us consider the expression of the voltage waveform of a single-phase system is:

Where V is the amplitude of the waveform, ω is the angular velocity of propagation of the wave.

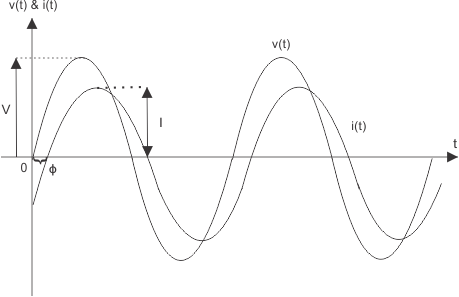
Now, consider the current of the system is i(t) and this current has a phase difference from the voltage by an angle φ. That means the current wave propagates with φ radiant lag in respect of the voltage. The voltage and current waveform can be represented graphically as shown below:

Now, let us plot the term P versus time,

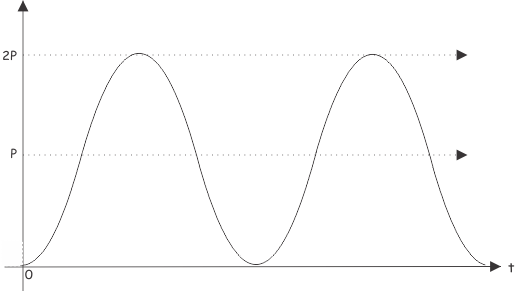
It is seen from the graph that, the term P does not have any negative value. So, it will have a nonzero average value. It is sinusoidal with a frequency twice of system frequency. Let us now plot the second term of the power equation, i.e. Q.

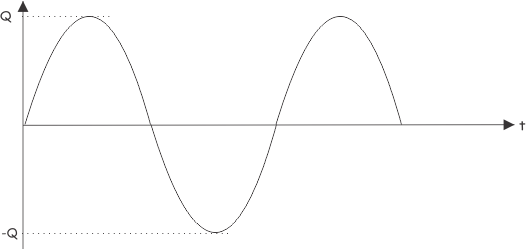
This is purely sinusoidal and has a zero average value. So from these two graphs, it is clear that P is the component of power in an AC circuit, which actually transported from network A to network B. This power is consumed in network B as electric power.

Q, on the other hand, does not really flow from network A to network B. Rather it oscillates between networks A and B. This is also a component of power, actually flowing into and out of the inductor, capacitor-like energy storage elements of the network.
Here, P is known as the real or active part of the power, and Q is known as the imaginary or reactive part of the power.

Hence, P is called real power or active power, and Q is called imaginary or active power. The unit of active power is Watt, whereas the unit of reactive power is Voltage Ampere Reactive or VAR.