Published by: Zaya
Published date: 26 Jun 2021
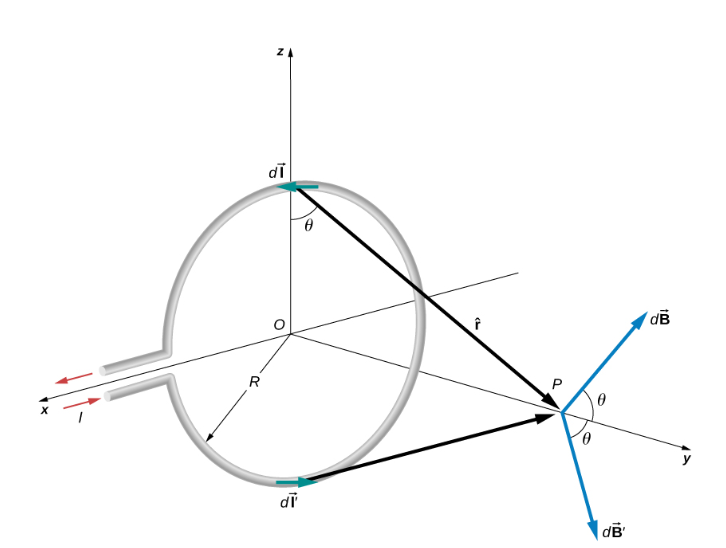
Figure 1:Determining the magnetic field at point P along the axis of a current-carrying loop of wire.
We can use the Biot-Savart law to find the magnetic field due to a current. We first consider arbitrary segments on opposite sides of the loop to qualitatively show by the vector results that the net magnetic field direction is along the central axis from the loop. From there, we can use the Biot-Savart law to derive the expression for the magnetic field.
Let P be a distance y from the center of the loop. From the right-hand rule, the magnetic field dB⃗ at P, produced by the current element Idl⃗, is directed at an angle θ above the y-axis as shown. Since dl⃗ is parallel along the x-axis and rˆ is in the yz-plane, the two vectors are perpendicular, so we have
where we have used r2=y2+R2.
Now consider the magnetic field dB⃗ ′ due to the current element Idl⃗ ′, which is directly opposite Idl⃗ on the loop. The magnitude of dB⃗ ′ is also given by Equation, but it is directed at an angle θ below the y-axis. The components of dB⃗ and dB⃗ ′ perpendicular to the y-axis therefore cancel, and in calculating the net magnetic field, only the components along the y-axis need to be considered. The components perpendicular to the axis of the loop sum to zero in pairs. Hence at point P:
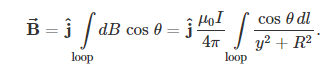
For all elements dl⃗ on the wire, y, R, and cosθ are constant and are related by
Now from Equation, the magnetic field at P is
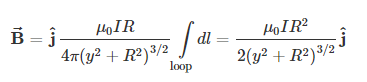
where we have used ∫loopdl=2πR. As discussed in the previous chapter, the closed current loop is a magnetic dipole of moment μ⃗ =IAnˆ. For this example, A=πR2 and nˆ=jˆ, so the magnetic field at P can also be written as