Published by: Zaya
Published date: 25 Jun 2021
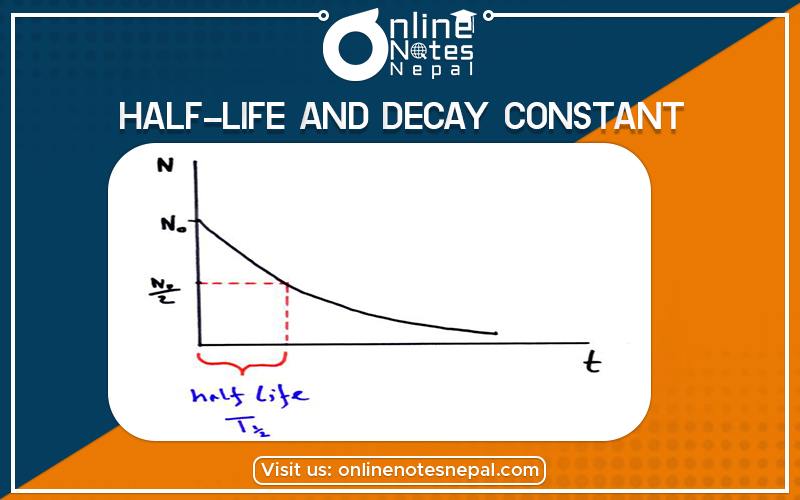
The Half-life and Decay Constant are explained below:
Half-life (symbol t1⁄2) is the time required for a quantity to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo, or how long stable atoms survive radioactive decay. The term is also used more generally to characterize any type of exponential or non-exponential decay. For example, the medical sciences refer to the biological half-life of drugs and other chemicals in the human body. The converse of half-life is doubling time.
The original term, half-life period, dating to Ernest Rutherford’s discovery of the principle in 1907, was shortened to half-life in the early 1950s. Rutherford applied the principle of a radioactive element’s half-life to studies of age determination of rocks by measuring the decay period of radium to lead-206.
Half-life is constant over the lifetime of an exponentially decaying quantity, and it is a characteristic unit for the exponential decay equation. The accompanying table shows the reduction of a quantity as a function of the number of half-lives elapsed.
The radioactive half-life for a given radioisotope is a measure of the tendency of the nucleus to “decay” or “disintegrate” and as such is based purely upon that probability. The tiny nuclear size compared to the atom and the enormity of the forces which act within it make it almost totally impervious to the outside world. The half-life is independent of the physical state (solid, liquid, gas), temperature, pressure, the chemical compound in which the nucleus finds itself, and essentially any other outside influence. It is independent of the chemistry of the atomic surface and independent of the ordinary physical factors of the outside world. The only thing which can alter the half-life is direct nuclear interaction with a particle from outside, e.g., a high energy collision in an accelerator.

The predictions of decay can be stated in terms of the half-life, the decay constant, or the average lifetime. The relationship between these quantities is as follows.

Note that the radioactive half-life is not the same as the average lifetime, the half-life being 0.693 times the average lifetime. The example that causes the most confusion is the decay of the free neutron with a half-life of 10.3 minutes and an average lifetime of 14.9 minutes.