The magnetic field at the axis of the circular current-carrying coil

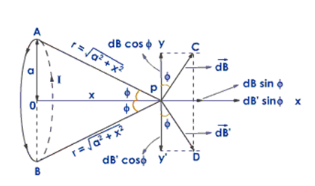
Consider a circular coil having radius a and centre O from which current I flows in the anticlockwise direction. The coil is placed at the YZ plane so that the centre of the coil coincide along X-axis. P be any point at a distance x from the centre of the coil where we have to calculate the magnetic field. let dl be the small current-carrying element at any point A at a distance r from the point P where

the angle between r and dl is 90°. Then from Biot-Savart law, the magnetic field due to current carrying element dl is

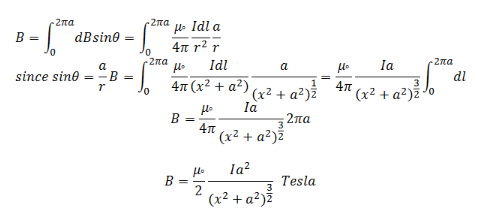
The direction of the magnetic field is perpendicular to the plane containing dl and r. So the magnetic field dB has two components

Similarly, consider another current-carrying element dl’ which is diametrically opposed to pointing A. The magnetic field due to this current carrying element dB’ also has two components

Here both dBcosθ and dB’cosθ are equal in magnitude and opposite in direction. So they cancel each other. Similarly, the components dBsinθ and dB’sinθ are equal in magnitude and in the same direction so they add up.

This is the expression for the magnetic field due to the circular current-carrying coil along its axis.