Bohr’s Theory of Hydrogen Atom

The great Danish physicist Niels Bohr (1885–1962) made immediate use of Rutherford’s planetary model of the atom. ([link]). Bohr became convinced of its validity and spent part of 1912 at Rutherford’s laboratory. In 1913, after returning to Copenhagen, he began publishing his theory of the simplest atom, hydrogen, based on the planetary model of the atom. For decades, many questions had been asked about atomic characteristics. From their sizes to their spectra, much was known about atoms, but little had been explained in terms of the laws of physics. Bohr’s theory explained the atomic spectrum of hydrogen and established new and broadly applicable principles in quantum mechanics.

Niels Bohr, the Danish physicist, used the planetary model of the atom to explain the atomic spectrum and size of the hydrogen atom. His many contributions to the development of atomic physics and quantum mechanics, his influence on many students and colleagues, and his integrity, especially in the face of Nazi oppression, earned him a prominent place in history. (credit: Unknown Author, via Wikimedia Commons)

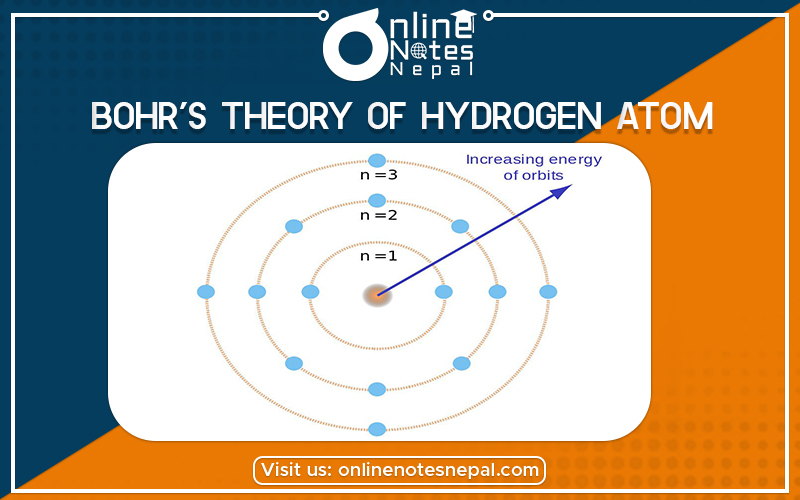
Bohr’s model of the hydrogen atom started from the planetary model, but he added one assumption regarding the electrons. What if the electronic structure of the atom was quantized? Bohr suggested that perhaps the electrons could only orbit the nucleus in specific orbits or shells with a fixed radius. Only shells with a radius given by the equation below would be allowed, and the electron could not exist in between these shells. Mathematically, we could write the allowed values of the atomic radius as r(n)=n^2\cdot r(1)r(n)=n
2
⋅r(1)r, left parenthesis, n, right parenthesis, equals, n, squared, dot, r, left parenthesis, 1, right parenthesis, where nnn is a positive integer, and r(1)r(1)r, left parenthesis, 1, right parenthesis is the Bohr radius, the smallest allowed radius for hydrogen.
He found that r(1)r(1)r, left parenthesis, 1, right parenthesis has the value
\text{Bohr radius}=r(1)=0.529 \times 10^{-10} \,\text{m}Bohr radius=r(1)=0.529×10 −10m

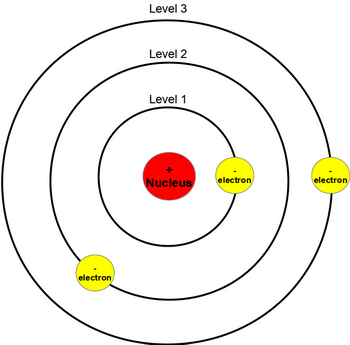
Fig: An atom of lithium shown using the planetary model.

By keeping the electrons in circular, quantized orbits around the positively-charged nucleus, Bohr was able to calculate the energy of an electron in the ninth energy level of hydrogen: E(n)=-\dfrac{1}{n^2} \cdot 13.6\,\text{eV}
E(n)=− n 21⋅13.6eVE, left parenthesis, n, right parenthesis, equals, minus, start fraction, 1, divided by, n, squared, end fraction, dot, 13, point, 6, start a text, e, V, end text, where the lowest possible energy or ground state energy of a hydrogen electron—E(1)E(1)E, left parenthesis, 1, right parenthesis—is -13.6\,\text{eV}−13.6eVminus, 13, point, 6, start a text, e, V, end text.
Note that the energy is always going to be a negative number, and the ground state, n=1n=1n, equals, 1, has the most negative value. This is because the energy of an electron in orbit is relative to the energy of an electron that has been completely separated from its nucleus, n=\inftyn=∞n, equals, infinity, which is defined to have an energy of 0\,\text{eV}0eV0, start a text, e, V, end text. Since an electron in orbit around the nucleus is more stable than an electron that is infinitely far away from its nucleus, the energy of an electron in orbit is always negative.