Biot-Savart Law

The Biot-Savart Law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current. Biot–Savart law is consistent with both Ampere’s circuital law and Gauss’s theorem. The Biot Savart law is fundamental to magnetostatics, playing a role similar to that of Coulomb’s law in electrostatics.

Biot Savart law was created by two French physicists, Jean Baptiste Biot and Felix Savart derived the mathematical expression for magnetic flux density at a point due to a nearby current-carrying conductor, in 1820. Viewing the deflection of a magnetic compass needle, these two scientists concluded that any current element projects a magnetic field into the space around it.
 

Through observations and calculations, they had derived a mathematical expression, which shows, the magnetic flux density of which dB, is directly proportional to the length of the element dl, the current I, the sine of the angle, and θ between the direction of the current and the vector joining a given point of the field and the current element and is inversely proportional to the square of the distance of the given point from the current element, r.

Biot Savart Law Statement

This is Biot Savart law statement:

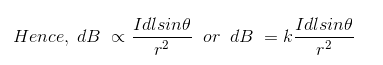
Where, k is a constant, depending upon the magnetic properties of the medium and system of the units employed. In the SI system of the unit,

Therefore, the final Biot Savart law derivation is,

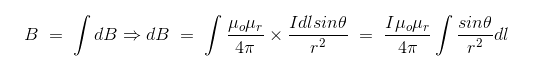
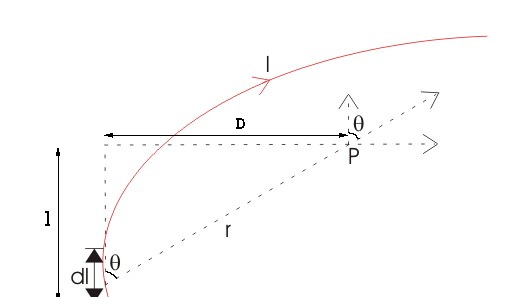
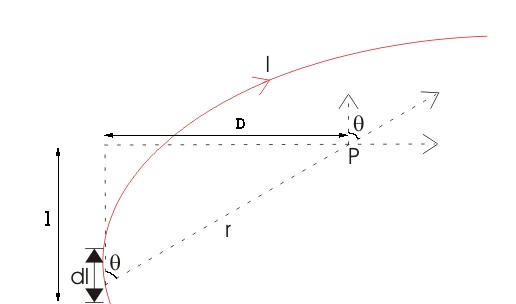
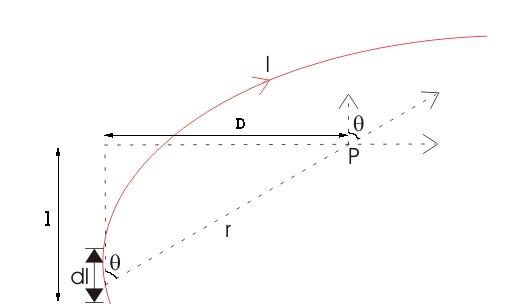
Let us consider a long wire carrying a current I and also consider a point p in the space. The wire is presented in the picture below, in red color. Let us also consider an infinitely small length of the wire dl at a distance r from the point P as shown. Here, r is a distance-vector that makes an angle θ with the direction of current in the infinitesimal portion of the wire.

If you try to visualize the condition, you can easily understand the magnetic field density at point P due to that the infinitesimal length dl of the wire is directly proportional to the current carried by this portion of the wire.

As the current through that infinitesimal length of wire is the same as the current carried by the whole wire itself, we can write,

It is also very natural to think that the magnetic field density at that point P due to that infinitesimal length dl of wire is inversely proportional to the square of the straight distance from point P to the center of dl. Mathematically we can write this as,

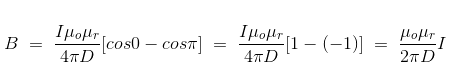
Lastly, magnetic field density at that point P due to that infinitesimal portion of the wire is also directly proportional to the actual length of the infinitesimal length dl of wire. As θ be the angle between distance vector r and direction of current through this infinitesimal portion of the wire, the component of dl directly facing perpendicular to the point P is dlsinθ Biot-Savart Law

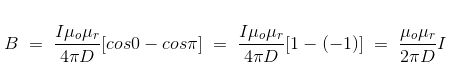
Now, combining these three statements, we can write,

This is the basic form of Biot Savart’s Law

Now, putting the value of constant k (which we have already introduced at the beginning of this article) in the above expression, we get

Here, μ0 used in the expression of constant k is absolute permeability of air or vacuum and its value is 4π10-7 Wb/ A-m in SI system of units. μr of the expression of constant k is the relative permeability of the medium.

Now, flux density(B) at the point P due to the total length of the current-carrying conductor or wire can be represented as,

If D is the perpendicular distance of the point P from the wire, then

Now, the expression of flux density B at point P can be rewritten as,

As per the figure above,

Finally, the expression of B comes as,

This angle θ depends upon the length of the wire and the position of the point P. Say for a certain limited length of the wire, angle θ as indicated in the figure above varies from θ1 to θ2. Hence, magnetic flux density at point P due to the total length of the conductor is,

Let’s imagine the wire is infinitely long, then θ will vary from 0 to π that is θ1 = 0 to θ2 = π. Putting these two values in the above final expression of Biot Savart law, we get,