The magnetic field along the axis of the solenoid

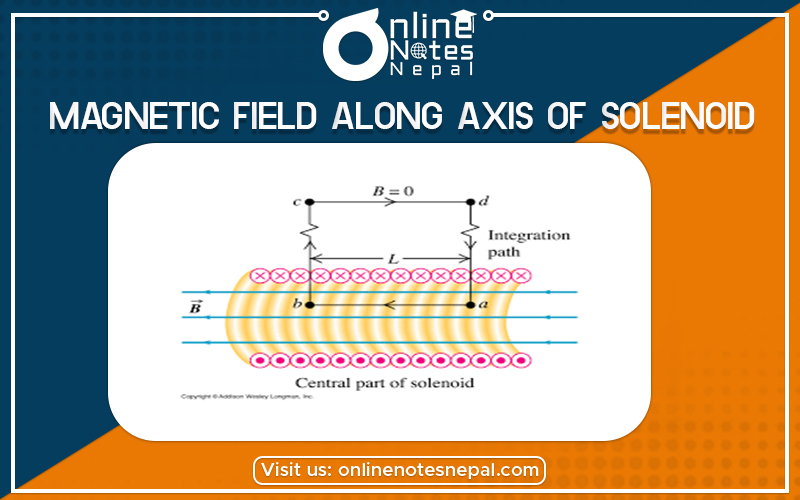
A solenoid is a ling cylindrical coil having a number of circular turns. Consider a solenoid having radius R consists of n number of turns per unit length. Let P be the point at a distance x̥ from the origin of the solenoid where we have to calculate the magnitude of the magnetic field. The current-carrying element dx at a distance x from the origin and a distance r from point P

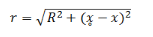
The magnetic field due to current carrying circular coil at any axis is

from the figure we have,

Now from the above three equations, we get,

Now total magnetic field can be obtained by integrating from Φ1 to Φ2, we get

Hence this expression gives the magnetic field at point p of the solenoid of finite length. For the infinite long solenoid
so,

This is the field on the axis of the solenoid. What happens if we move away from the axis? Is the field a little greater as we move away from the axis, or is it a little less? Is the field a maximum on the axis, or a minimum? Or does the field go through a maximum, or a minimum, somewhere between the axis and the circumference? We shall answer these questions in section