Mean or Average value of AC

The current and voltage in a DC system remain constant over a period of time so that there is no problem in specifying their magnitudes. However, an alternating current or voltage varies from time to time. Then a question arises on how to express the magnitude of an alternating current or voltage. Though there are many ways of expressing it, we limit our discussion to two ways, namely mean value and RMS (Root Mean Square) value of AC.

We have learned that the magnitude of an alternating current in a circuit changes from one instant to another instant and its direction also reverses for every half cycle. During the positive half cycle, the current is taken as positive and during the negative cycle, it is negative. Therefore the mean or average value of symmetrical alternating current over one complete cycle is zero.

Therefore the average or mean value is measured over one-half of a cycle. These electrical terms, average current, and average voltage can be used in both AC and DC circuit analysis and calculations.

The average value of alternating current is defined as the average of all values of current over a positive half-cycle or negative half-cycle.

The instantaneous value of sinusoidal alternating current is given by the equation i = I m sin ω t or i = I’m sinθ (where θ = ωt) in the given figure:

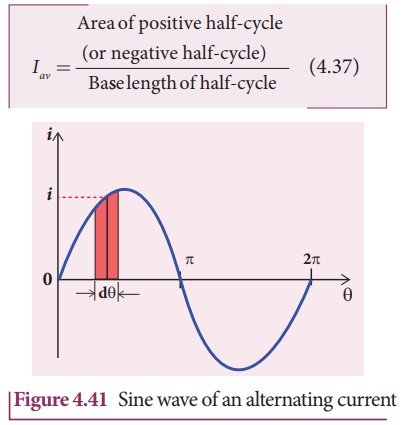
The sum of all currents over a half-cycle is given by the area of positive half-cycle (or negative half-cycle). Therefore,

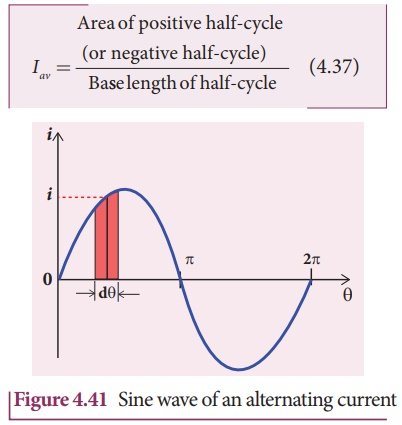
Consider an elementary strip of thickness dθ in the positive half-cycle of the current wave (Figure 4.41). Let i be the mid-ordinate of that strip.

Area of the elementary strip = i dθ

Area of positive half-cycle

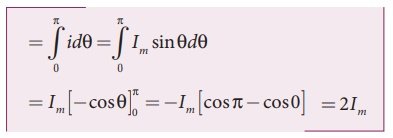
Substituting this in equation (4.37), we get (The base length of half-cycle is π)

The average value of AC, Iav = 2Im/πHence the average value of AC is 0.637 times the maximum value Im of the alternating current. For negative half-cycle, av = −0.637 Im .